Hot issues:
This module collects the frequently encountered and difficult problems for reference only.
This module collects the frequently encountered and difficult problems for reference only.
Current location:Hot issues > Answer
在$\triangle ABC$中,$AB=AC$,$BD$平分$\angle ABC$,交$AC$于点$D$,若$BD=BC$,求$\angle A=?$
如图,
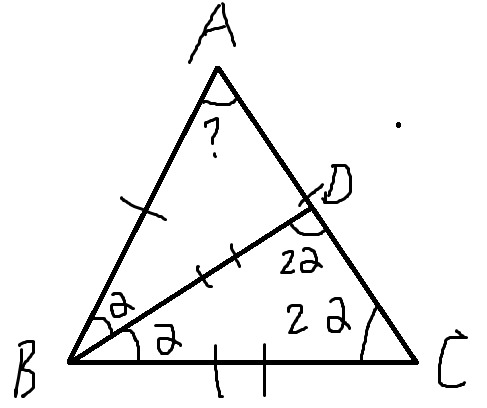
设$\angle ABD=α$,则: \begin{align} \angle CBD=&α\\ \angle BCD=&2α\\ \angle CDB=&2a \end{align} 因为$\triangle BCD$的内角和为$180°$,所以 \begin{align} &\angle BCD+\angle CDB+\angle DBC=180°\\ =>\ &2α+2α+α=180°\\ =>\ &α=36° \end{align} 又因为$\triangle ABC$的内角和也是$180°$,所以有 \begin{align} &\angle A+\angle B+\angle C=180°\\ =>\ &\angle A + 2α+2α=180°\\ =>\ &\angle A+4α=180°\\ =>\ &\angle A=180°-4α\\ =>\ &\angle A=180°-4 \times 36°\\ =>\ &\angle A=36° \end{align} 即,所求的角$A$为:$\angle A=36°$
