解：
         如图所示：

   
        
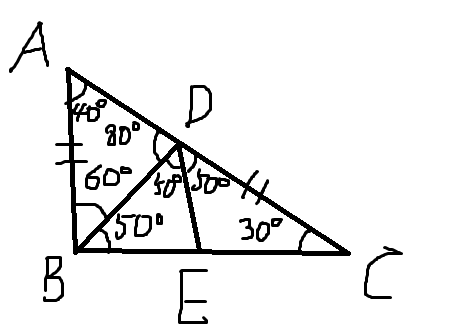
作$\angle BDC$的平分线交$BC$于$E$点，则： $$ \begin{align} \angle BCD=&30°\\ \angle CDE=&50°\\ \angle EDB=&50°\\ \angle DBE=&50°\\ \angle BDA=&80°\\ \angle BAD=&40° \end{align} $$ 在$\triangle ABD$中，由正弦定理得： $$ \frac {AB}{sin80°}=\frac{BD}{sin40°}\ \ \ \ (1) $$ 在$\triangle BCD$中，由正弦定理得： $$ \begin{align} \frac {BD}{sin30°}=&\frac{CD}{sin50°}\\ \ \ \ \ =>BD=&\frac{sin30°}{sin50°}\times CD\ \ \ \ (2) \end{align} $$ 将$(2)$代入$(1)$消去$BD$得： \begin{align} \frac {AB}{sin80°}=&\frac {sin30°}{sin40°\times sin50°}\times CD\\ => AB=&\frac{sin80°\times sin30°}{sin40°\times sin50°}\times CD\\ =&\frac{sin80°\times sin30°}{-\frac 12(cos90°-cos10°)}\times CD\\ =&\frac{sin80°\times sin30°}{\frac 12cos10°}\times CD\\ =&CD \end{align} 即$AB=CD$，原命题得证。