解：
         如图：




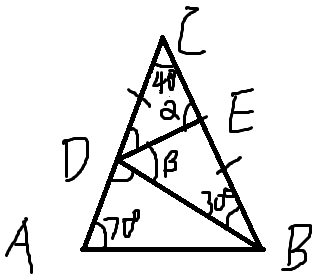
因为 $$\angle A＝\angle ABC＝\angle ADB＝ 70°$$ ，所以， $$\begin{align} \angle C=& 40°\\ \angle ADB=& 70°\\ \angle ABD=& 40°\\ \angle DBE=& 30° \end{align}$$ 设$\angle BDE=β$，$\angle CED=α$，则 $$\angle α=\angle β+30°\ \ \ \ (1)$$ 则在$\triangle CDE$中，由正弦定理得： $$\frac {DE}{sin40°}=\frac{CD}{sinα}\ \ \ \ (2)$$ 在$\triangle BDE$中，由正弦定理得： $$\frac {BE}{sinβ}=\frac{DE}{sin30°}\ \ \ \ (3)$$ 由$(3)$得： $$DE=\frac{BE \times sin30°}{sinβ}\ \ \ \ (4)$$ 把$(4)$代入$(2)$得： $$\frac{BE \times sin30°}{sin40° \times sinβ}=\frac{CD}{sinα}\ \ \ \ (5)$$ 因为$CD=BE$，所以等式可以化简为： $$sin30° \times sinα=sin40°\times sinβ\ \ \ \ (6)$$ 再把$(1)$代入$(6)$得： $$sin30°\times sin(β+30°)=sin40°\times sinβ$$ 解这个三角函数方程得： $$β=50°$$
         即：$\angle BDE=50°$